我们通过剖析That flight 来研究这个过程。假设在That flight中That已经被识别出来，当时的状态如下：

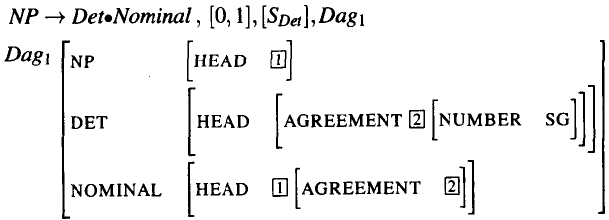
现在来研究下面的情况，这时剖析器已经处理了flight，并由此产生了如下的状态：

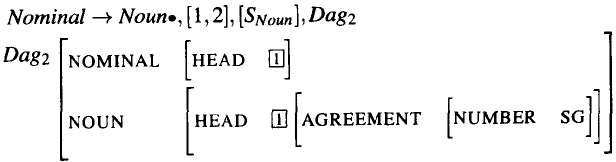
为了推进NP规则，分析器把在Dag2的NOMINAL特征中发现的特征结构与在NP的Dag1的NOMINAL特征中发现的特征结构进行合一。正如在原来的算法中那样，我们建立起一个新状态来表示现有状态已经被向前推进这一事实。这个新状态的DAG也就是上面合一的结果所形成的DAG。

对于原来算法的最后一个改变是检查已包含在线图中的状态。在原来的算法中，ENQUEUE这个功能拒绝进入线图中的与该线图已有的状态“等同”（identical）的任何状态。所谓“等同”意味着规则相同，开始位置和结束位置相同，点“.”的位置相同。这种检查使得算法可以避免与左递归规则相关的无穷递归问题。

在带合一约束的剖析中，我们的状态当然会更复杂，因为这时的状态中具有与其相关联的特征结构。在原来的标准看来似乎等同的状态，现在事实上可能是不同的，因为与它们联系的DAG可能有所不同。要解决这样的问题显然只需要扩充等同性的检查，使得这种检查包含与状态有关联的DAG，不过我们还可以改善这种解决办法。

之所以要求改善，是因为要进行等同性的检查。这种改善的目的在于阻止把无用状态加到线图中，以免造成浪费，这种改善对于剖析的影响可由现有状态来实现。换言之，我们希望阻止那些造成重复工作的状态进入线图中，这些工作最终可以由其他状态来完成。当然，很显然这是关于等同状态的问题，但这也是线图中的状态的问题，这个问题比研究新状态更具有一般性我们来研究下面的情况，其中线图包含的状态的Dag没有对Det进行约束。

NP → •Det NP, [i, i], [], Dag

这样的状态只是说，它期待在位置i有一个Det，任何的Det都可以做到这一点。

现在来研究如果剖析器试图把一个新状态插入到线图中，而线图中的状态与这个状态完全等同，只是DAG限制Det为单数时的情况。在这样的场合，尽管有关状态不等同，但是在线图中添加新状态不能得到什么东西，因此这样的插入被阻止。

为了看到这一点，让我们来考虑所有的情况。如果添加一个新状态，则单数Det在两个状态中都是匹配的，而且两个状态都要向前推进。由于特征的合一，两个状态都有DAG指出它们的Det都是单数，其结果是线图中的状态成倍增加。如果遇到复数的Det，那么新状态将拒绝这个Det，并且不向前推进，而这时老的规则将向前推进，进入线图中的一个新状态。另一方面，如果不把新状态放入线图中，复数或单数的Det将与更一般的状态相匹配，并且向前推进，这将导致把一个新状态加到线图中。注意，除了避免成倍增加状态的数目之外，这种情况与把新状态加到线图中的情形是完全一样的。总而言之，把一个比在线图中的状态更加特殊的状态加到线图中，最后还是一无所获。

可喜的是，我们可以使用前面讨论过的“蕴涵于”（subsumption）的概念，形式化地描述特征结构中的“一般化”（generalization）和“特殊化”（specialization）之间的关系。这意味着，改变ENQUEUE的一种合适的办法是检查一个新建立的状态是不是蕴涵于线图的任何现有状态中。如果是，就不允许它进入线图中。更具体地说，如果一个新状态与现有状态的规则相同，开始和结束位置相同，子部分相同，点“·”的位置相同，并且如果存在状态的DAG蕴涵于新状态的DAG（也就是说，DagwuDagmew),那么这个新状态就不能加到线图中。对于原来的Earley的ENQUEUE过程的必要改变，可参见图2。

责任编辑：admin