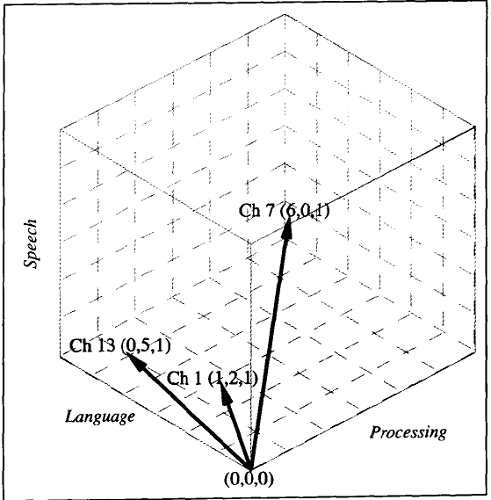
图17.3 由第1章、第7章和第13章的章节标题文字组成的文档所表示的简单三维向量空间

遗憾的是，在向量空间的这个实例中过于强调每个文档的各个坐标的绝对值。例如，Doc7的speech维度的重要性并不在于它的值是6，而是它是文档意义的最主要的贡献者。类似地，Doc1的具体值1，2和1并不重要，重要的是这3个维度具有大致相似的权重。例如，假定一个新文档的权重为3，6和3，则尽管检索词权重的大小不同，仍可以感觉到它与Doc1非常接近。

我们可以通过归一化（normalizing）文档向量来实现这个结果。简单地说，“归一化”这个术语指把所有向量转换为标准长度。通过把向量的每个维度都除以向量的总长度（定义为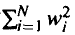），可以将它转换为单位长度。这实际上消除了空间中一个文档的确切长度的重要性，而强调文档向量相对原点的方向。

将该技术用于我们的3个样例文档，则可以得到下面的检索词乘文档矩阵A，这里的列表示Doc1，Doc7和Doc13，而行表示检索词speech, language和processing:

可以验证得到：采用这种方案，Doc1和假定的（3,6,3）文档的归一化向量最终是相同的。

现在回到确定向量之间相似性的主题。将早先给出的相似性公式中的二元值更新为数值的权重，则得到下面的方程：

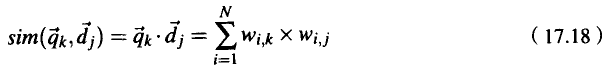
这个方程表示向量之间的点乘（dot product）。通常，两个向量之间的点乘并不用做相似性的度量，因为它对于各种维度的绝对大小过于敏感。然而，已经归一化的向量之间的点乘具有一个有用并且直观的解释：它计算的是两个向量之间夹角的余弦。当两个文档相同时，它们的余弦值是1；而当它们正交时（没有共同的检索词），它们的余弦值则是0。

注意，如果由于某些原因向量没有被存储为归一化的形式，那么该归一化可以直接引入下面的相似性计算公式：

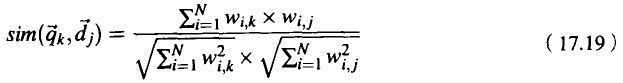
当然，在文档集相对稳定并且需要对许多查询条件进行处理的情形下，一次性归一化文档向量并存储它们，比在相似性计算时引入归一化更合理。

让我们来讨论在一些小例子背景下相似性度量是如何进行的。研究下面特意选出的由speech，language和processing组成的查询条件。将这个查询条件转换为一个向量并把它归一化，则可以得到向量（0.57，0.57，0.57）。计算该向量和3个文档向量之间的余弦，可以得出它与Doc1最接近（余弦值是0.92），接着是Doc13（余弦值是0.67），最后是Doc7（余弦值是0.65）。这个顺序与我们关于该查询条件和这些文档之间的关系的直觉是十分接近的。

现在来研究一个较短的只包含检索词speech和processing的查询条件。处理这个查询条件，以生成归一化的向量（0.70,0,0.70）。计算这个向量和我们的文档之间的余弦，现在Doc7最接近（余弦值是0.80），接着是Doc1（余弦值是0.58），而Doc13最远（余弦值是0.13）。

责任编辑：admin