证明一种语言是正则语言的最普通的方法是为这种语言实际地建立起正则表达式。我们可以根据正则语言对于并运算、毗连运算、Kleene星号运算、补运算、交运算等都是封闭的这种特性来进行这样的证明。如果能够为一种语言中的两个不同部分独立地建立起正则表达式，就可以使用并运算的运算子为整个语言建立正则表达式，并且证明这种语言是正则语言。

有时，我们试图证明一种语言不是正则语言。证明这种情况的最有用的工具是抽吸引理(pumping lemma）。这个引理的后面有两种直觉，对于抽吸引理的描述来自Lewis and Papadimitriou（1981）以及Hopcroft and Ullman(1979）。第一个直觉是，如果一种语言能够被有限状态自动机模拟，那么我们必定能够根据这种记忆约束量来判定任何符号串是不是在该语言中。这个记忆约束量对于不同的符号串不会增长得很大（因为对于给定的自动机，它的状态数目是固定的），因此这个记忆量不一定与输入的长度成比例。这意味着，诸如aⁿbⁿ这样的语言不可能是正则语言，因为这时我们需要某种办法来记住n的数目，以便保证符号串中a的数量与b的数量相等。第二个直觉依赖于这样的事实：如果一个正则语言具有任意长的符号串（比自动机中的状态数还长），那么在该语言的自动机中必定会存在某种回路（loop）。我们可以使用这样的事实说明，如果一种语言没有这样的回路，它就不是正则语言。

让我们来研究一种语言L和与它相应的确定有限自动机M，M具有N个状态。考虑输入符号串的长度也是N。这个机器从状态q0开始，在读了一个符号之后进入状态q1，在读了N个符号之后进入状态qn。换言之，长度为N的符号串将通过N+1个状态（从状态q0到状态qN）。但是，在机器中只有N个状态。这意味着，在接收的路径上至少有两个状态必须是相同的（把它们称为qi和qj）。换句话说，在从开始状态到最后状态的接收路径上，必定存在回路。图1说明了这种情况。设x是机器从开始状态q0到回路起点的状态qi读的符号串，y是机器通过回路时读的符号串，z是从回路终点qj到最后的接收状态qN读的符号串。

机器接收由这三个符号x,y和z构成的毗连。但是，如果机器接收了xyz，那么它一定也接收xz！这是因为机器在处理xz时可以跳过回路，y就像被抽水机抽吸了一样。另外，机器也可以在回路上打任意次数的圈儿，这样它也就可以接收xyyz，xyyyz和xyyyyz等；这时，y又被放出来了。事实上，当n≥0时，它可以接收形式为xyⁿz的任何符号串。

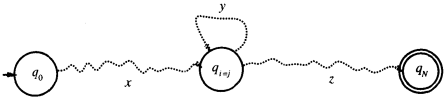
图1 具有N个状态并且接收含有N个符号的符号串xyz的机器

这里给出的抽吸引理是有限状态语言中的一种简化版本。比较强的版本也可以应用于有限状态语言，但是它的抽吸引理的特定更明显。