如果我们对于每匹马的概率估计都是一样的，情况将如何呢？前面我们已经看到，如果对于每匹马都使用等长的二进制编码，每匹马都用3比特来编码，因此平均的比特数为3。这时的熵是一样的吗？是的，在这种情况下，每匹马的估计概率都是1/8。我们选择马的熵是这样计算的：

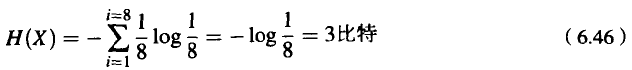
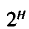这个值称为困惑度。从直觉上，我们可以把困惑度理解为在随机实验中选择随机变量的加权平均数。因此，在等概率估计的8匹马之间进行选择时（这时熵H=3比特），困惑度是2³，也就是8。在概率有差异的8匹马之间进行选择时（这时熵H=2比特），困惑度是2²，也就是4。

前面计算的是单个变量的熵。然而，我们在很多场合需要计算序列的熵。例如，对于一个语法来说，我们需要计算单词的序列W={…W0.W1,W2,…，Wn.}的熵。我们的办法之一是让变量能够覆盖单词的序列。例如，我们可以计算在语言L中长度为n的单词的一切有限序列的随机变量的熵。

计算公式如下：

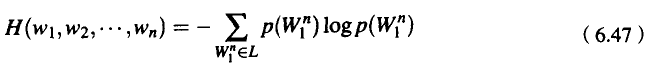
我们可以把熵率（entropy rate）定义为用单词数来除这个序列的熵所得的值（我们也可以把熵率想像成每个单词的熵）：

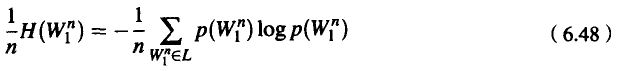
但是，为了计算一个语言的真正的熵，我们需要考虑无限长度的序列。如果我们肯把语言想像成产生单词序列的随机过程L，那么它的熵率H(L）可定义为：

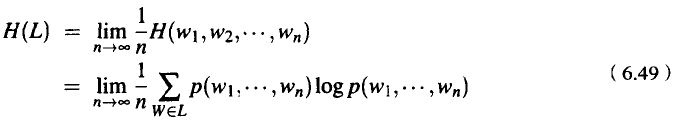
Shannon-McMillan-Breiman定理(Algoet and Cover,1988;Cover and Thomas,1991)指出， 如果语言在某种意义上是正则的（确切地说，如果语言既是平稳的又是遍历的），那么有：

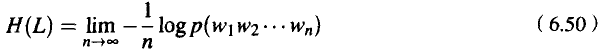
这意味着，我们可以取语言中一个足够长的序列来替代该语言中所有可能的序列的总和。Shannon-McMillan-Breiman定理的直觉解释是：一个足够长的单词序列可以在其中包含其他很多较短的序列，而且每个这样的较短的序列都可以按照它们各自的概率重复出现在较长的序列中。

如果随着时间的推移，随机过程指派给序列的概率不变，则可以认为这个随机过程是平稳的。换言之，在平稳随机过程中，单词在时间t的概率分布与在时间t+1的概率分布是相同的。马尔可夫模型以及N元语法的概率分布都是平稳的。例如，在二元语法中，P只依赖于P，因此如果把时间的索引号移动到X，Pi+x仍然依赖于Pi+x-l。然而自然语言却不是平稳的，在自然语言中，下一个单词的概率可能依赖于任意距离的事件并且依赖于时间。所以，我们的统计模型对于自然语言的正确分布和熵的描述都是近似的。

最后，使用这种尽管不正确但却非常方便的简单假设，我们就能够取一个很长的输出样本来计算某个随机过程的熵，并且计算它的平均对数概率。

责任编辑：admin