为什么要关心英语的熵呢？第一个原因是英语的真正的熵将为我们将来对概率语法的试验提供一个可靠的下界。另一个原因是我们可以利用英语的熵值帮助理解语言中的哪一部分提供的信息最大。例如，判断英语的预测能力主要依赖于词序、语义、形态、组成成分还是语用线索。这样可以在很大程度上帮助我们了解语言模型应该着重研究哪一方面。

计算英语熵值的方法通常有两种。第一种方法是Shannon(1951)使用的方法，这是Shannon在信息论领域的开创性工作的一部分，其思路是利用受试人来构造一个信息试验，要求受试人来猜测字母，观察猜测的字母中有多少是正确的，从而估计字母的概率，然后估计序列的熵值。

实际的试验是这样来设计的：我们给受试人看一个英语文本，然后要求受试人猜测下一个字母。受试人利用他们的语言知识来猜测最可能出现的字母，然后猜测下一个最可能的字母，依次类推。我们把受试人猜对的次数记录下来。Shannon指出，猜测数序列的熵与英语的熵是相同的。其

直觉解释是：如果受试人进行n个猜测，那么，给定猜测数序列，我们能够通过选择第n个最可能的字母的方法，重建原来的文本。这样的方法要求猜字母而不是猜单词（因为受试人有时必须对所有的字母进行穷尽的搜索），所以Shannon计算的是英语中每个字母的熵，而不是英语中每个单词的熵。他报告的结果是：英语字母的熵是1.3比特（对于27个字母而言，包括26个字母以及空白）。Shannon 的这个估值太低了一些，因为他是根据单篇的文本（Dumas Malone的Jefferson the Virginian）来进行试验的。Shannon还注意到，对于其他的文本（例如新闻报道、科学著作和诗歌），他的受试人往往会猜错（因此这时的熵比较高）。最近有人模仿Shannon做了类似的试验，他们以赌场为例，让受试人对下一个出现的字母打赌（Cover and King,1978;Cover and Thomas,1991）。

第二种计算英语的熵的方法有助于避免导致Shannon结果失误的单篇文本的问题。这个方法使用一个很好的随机模型，在一个很大的语料库上训练这个模型，用它给一个很长的英语序列指派一个对数概率，计算时使用Shannon-McMillan-Breiman定理：

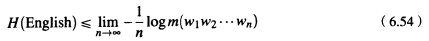
例如，Brown et al.（1992）在58300万单词的英语文本上（293181个“型”）训练了一个三元语法模型，用它来计算整个Brown语料库的概率（1014312个“例”）。训练数据包括新闻、百科全书、小说、官方通信、加拿大议会论文集以及其他各种资源。

然后，他们使用词的三元语法给Brown语料库指派概率，把语料库看成是一个字母序列，从而计算Brown语料库的字符的熵。他们得到的结果是：每个字符的熵为1.75比特（这里的字符集包含了95个可印刷的全部ASCII字符）。

根据报告，英语书面文本中单词（包括空白）的平均长度是5.5个字符（Nadas,1984）。如果这个报告的数值是正确的，就意味着在普通的英文中，Shannon估计的每个字母的熵为1.3比特将对应于每个单词的困惑度为142。前面报告的WSJ试验的困惑度数值明显低于这个数值，其原因在于训练集和测试集都来自英语的同样的子样本。这样就表明这个试验低估了英语的复杂性，因为华尔街日报看起来确实很不像莎士比亚的著作。

责任编辑：admin