即使说话者和听者都没有看见这辆车或者没有确认它,这句话的意思也是很容易理解的。这种不定指性描述词“acar”证实车的存在,代词“it”用来增加这辆车的信息。这一语句很好理解,即使谁都不知道这辆车的情况。那么,当不知道要指代的对象时,在知识库中应怎样表示这个常数呢?面对这样的问题,一些研究人员讨论了完全不同层次的表示篇章实体的方法。不过在这里,我们采用了一种简单方法,也就是使用Skolem函数来表示篇章实体。需要记住的是,Skolem函数(或Skolem常量)只是引入到表示语言中的一个新的术语。在可能的情况下,我们将逻辑形式中引入的篇章标记作为新的Skolem常量。这样,如果“a car”的逻辑形式为<A c1 CAR>,那么产生的Skolem常数就是C1。共指用等式来表示。这样,如果一个代词“it”的逻辑形式为(PRO i1 IT1),那么,它与C1之间是共指关系这个事实就表示为(I1=C1)。
1. 生成篇章实体
与子句的解释类似,通常,每一个名词短语都要生成一个篇章实体。不同的名词短语对各自生成的篇章实体赋予不同的约束。一个不定指性名词短语往往生成一个新的篇章实体,在知识库中不需要进一步标识。而一个专有名称通常描述一个已经在知识库中定义的与该名称相关的对象。一个定指性名词短语(包括代词)一般指一个篇章中已经涉及的一个对象,通常是局部上下文中的篇章实体。复数名词短语产生一系列对象。一个包含连词的复杂名词短语引发一个包含所有并列成分的集合。例如,名词短语“John and Mary”引发三个篇章实体:John1, Mary1和集合{John1, Mary1}。
这类短语非常重要,因为不定指性名词短语引入了很多新的篇章实体,并且提供了处理定指性指代的更多背景。为了计算出篇章实体的集合,我们首先将逻辑表达式转换为12.4节中的量词表示形式,使用明确的集合,将所有自然语言的量词化简为全称和存在量化表示形式。对于这个简单的例子来说,我们假定所有的专有名称和定指性名词短语都已经用知识库中表示所指代对象的常量替换掉了。
对于复数名词短语,无论是解释为一个整体,还是解释为多个个体,都要引发同一个集合。解释为一个整体时,这个集合直接在命题中用做一个参数;而解释为多个个体时,这个集合作为全称量词所指的范围。要定义这个集合,修饰语的转换相应地也必须分为两类,分别是对整个集合的约束(SR)和对集合中每一个个体的约束(IR)。例如,下面句子中的名词短语“Three boys”的转换:
9. Three boys lifted Fido.(三个男孩抬起了Fido。)
将引入一个SR,表示这个集合有三个元素,以及一个IR,断言其中每一个元素都是一个孩子。图1 对一些不定指性名词短语的转换进行了总结。
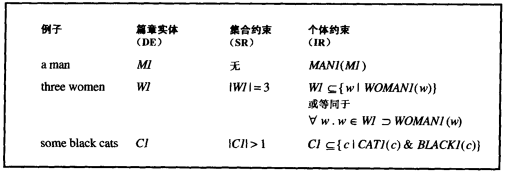
图1 不定指性名词短语的转换
2. 全称量词辖域内的不定指性名词短语
当一个不定指性名词短语出现在一个表示个体的全称量词的辖域内时,问题就复杂了。例如,在一个全称量词辖域内的单个不定指性名词短语引发的是一个集合而不是一个个体。比如下面的例子:
10a. Three boysi each bought a pizaj.(三个男孩每人买了一张比萨。)
10b. Theyi ate themj in the park.(他们在公园中吃掉了它们。)
值得注意的是,“Theyi ate itj in the park”不是句子10a的合理延续句。需要用什么属性来定义句子10a中的“a pizza”所生成的篇章实体呢?集合{x|Piza(x)}太笼统,句子10b中的“themj”也不能指所有比萨的集合。较好的办法是,“a pizza”为一个新的篇章实体P1,表示{xlPizza (x)}的子集。基于这一解释,句子10b中的“themj”指上一个句子中提到的比萨的集合。但是这一方法也会丢失P1内容的信息,即P1由是句子10a中提到的男孩所买的比萨组成的集合。P1的表达可以从句子10a的最初形式中推理得到:
∀ b:b∈ B1.
ヨp: Pizza(p). Buy(b, p) where I B1 l =3 & B1 ⊆{xI Boy(x)}
Skolem化的形式为:
∀ b:b∈ B1. Pizza(sk4(b)) & Buy1 (b, sk4(b))
其中,sk4(b)是新函数,用于产生每个男孩所买的比萨。这样,集合P1可以定义为由这个新函数产生的比萨的集合:
P1={x| Pizza(x)& ヨy:y∈B1.x=sk4(y)}
这个公式准确表示了这些男孩买的那些比萨。这个句子的完整分析过程如图2所示。

图2 由句子“Three boys each bought a pirzza”所生成的篇章实体
责任编辑:admin
上一篇:一个基于历史记录列表的简单回指模型
下一篇:综合的知识表示方法

微信公众号搜索“译员”关注我们,每天为您推送翻译理论和技巧,外语学习及翻译招聘信息。