项的区分度
2023-01-06 09:24:20 etogether.net 网络 次
项的区分度的方法最初是由H.P. Luhn提出的。假设Di和Dj表示两个文档，每个文档都是一组项组成的集合。用Sim(Di, Dj）表示两个文档之间的相似度，相似度取值范围为[0,1]。如果两个文档符合得很好，则相似度取1；而如果两个文档几乎没有共同之处，相似度取0；否则取中间值。
将文档集中所有文档间的相似度Sim(Di,Dj)（i≠j)都计算出来，则可得到文档集的平均文档相似度
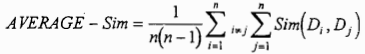
上式表示了文档空间的“密度”，即文档之间结合的程度。
文档空间密度还可以通过称作文档重心（Centroid）的文档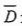
来表示。在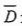
中，所有的项都用该项在文档集中的平均频数来表示：
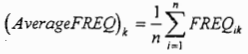
这样文档密度可表示为
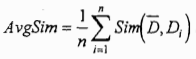
现在假设将项Tk从所有的文档表示中移去，用(AvgSim)k表示此时的空间密度。如果该项出现频数较高，并且分布比较均匀，它就可能出现在大部分文档中，去掉该项将会降低平均相似度，用这种项作为表示文档的索引项显然不合适。相反如果项Tk在一些文档中具有较高频数而在另一些中几乎不出现，它的消除将会增加平均相似度。
这样区分度DV可定义如下：
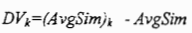
计算出所有项的区分度，并且按其值从大到小排列，我们可以得到三种类型的项：
（1）具有较好的区分度的项，其DV值为正值，它们的引入会降低空间密度（如图1）。
（2）一般的项，其DVk值接近于0，它们的引入或消除对平均相似度没有影响。
（3）具有较差区分度的项，其DVk值为负值，它们的引入使文档间的相似度增加。
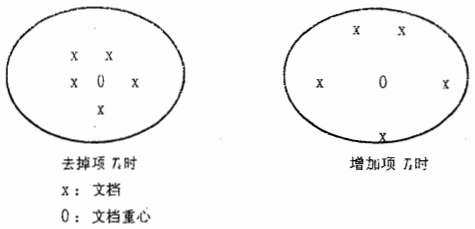
图1具有好的区分度的项示例
利用项的区分度公式，考虑到项Tk在文档Di中的项频FREQk，可定义项Tk在文档Di中的权重评价函数如下：
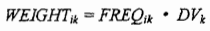
责任编辑：admin
上一篇：项的分类和分类词典
下一篇：向量空间模型
微信公众号搜索“译员”关注我们，每天为您推送翻译理论和技巧，外语学习及翻译招聘信息。