有相当数量的单词和词语具有所谓“创造世界的能力”（world creating ability）。之所以说“创造世界的能力”，是因为它们的意义表示包含的逻辑公式并不一定在现实世界中真实存在，而是某个假设世界中的东西。具有这种“创造世界的能力”的单词有believe, want, imagine 和know等。这些具有创造世界的能力的单词通常都采用各种类似于句子的成分作为它们的论元。

我们来研究如下的例子：

I believe that Mary ate British food.   （1）

应用面向事件的方法，可以说这个句子中有两个事件：一个是believing事件，这个事件是关于说话者的某个特定信念，另一个是eating事件，这个事件说明信念的东西是什么。不管时间信息，应用把事件具体化的方法，可以得到如下的意义表示：

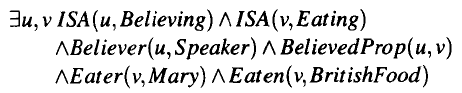
这样的表示看起来似乎比较直接，所有参与的角色都表示出来了，而且两个事件也合情合理地结合在一起了。但是，在这种连接的表示中，所有的连接部分都必须为真。在这样的场合，其结果是一个命题，即an eating of British food by Mary。具体地说，删除连接符号把这个公式分解成不同的公式，可以造出如下的公式：

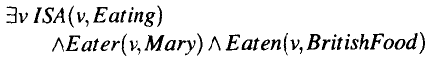
这种表示比我们想说的还清楚。说话者相信这个命题的事实并不能使这个命题成为真命题；这个命题只是在说话者的信念所表示的世界中才是真的。我们所需要的是具有相似结构的表示，而其中要给事件Eating一个特殊的地位。

注意，恢复到简单谓词表示是无济于事的。在使用这种谓词表示来表达句子时，最常见的错误是采用如下的表示：

Believing (Speaker, Eating (Mary, BritishFood))

这种表示的问题在于它不是有效的FOPC。谓词Believing的第二个论元应该是一个FOPC项，而不是一个公式。这种句法错误反映了一个深刻的语义学问题。在FOPC中谓词应该在所模拟领域的客体之间成立，而不能在所模拟领域的客体的关系之间成立。因此，FOPC缺乏有意义的手段来表示完整的命题之间的关系，而这种关系恰恰是单词believe, want, imagine和know等所要表示的。

处理这种情况的标准办法是使用算符（operator）来增强FOPC，使我们能够做出全逻辑公式的命题。让我们来研究如何使用这种方法来处理例句（1）。我们可以引入一个称为Believes的算符，取两个FOPC公式作为它的论元。一个公式指派一个believer，另一个公式指派所相信的命题。使用这个算符可以得到如下的意义表示：

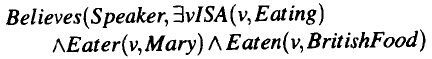
使用这样的方法，单词Believes对这个意义表示的贡献完全不是一个FOPC命题，而是一个可应用于所相信命题的算符。因此，这些“创造世界的动词”在语义分析中所起的作用与一般的像eat这样的普通动词很不相同。