程序清单1-1中的另一个函数是1wlrTest()，用于为数据集中每个点调用1wlr(），这有助于求解k的大小。

下面看看实际效果，将程序清单1-1的代码加入到regression.py中并保存，然后在Python提示符下输入如下命令：

>>> reload(regression)

<module 'regression' from 'regression.py'>

如果需要重新载入数据集，则输入：

>>>xArr,yArr=regression.loadDataSet('ex0.txt')

可以对单点进行估计：

>>> yArr[0]

3.1765129999999999

>>> regression.lwlr(xArr[0],xArr,yArr,1.0)

matrix([[ 3.12204471]])

>>> regression.lwlr (xArr [0],xArr,yArr,0.001)

matrix([[ 3.20175729]])

为了得到数据集里所有点的估计，可以调用1wlrTest（）函数：

>>> yHat = regression.lwlrTest (xArr, xArr, yArr,0.003)

下面绘出这些估计值和原始值，看看yHat的拟合效果。所用的绘图函数需要将数据点按序排列，首先对xArr排序：

xMat=mat(xArr)

>>> srtInd = xMat[:,1].argsort(0)

>>> xSort=xMat [srtInd][:,0,:]

然后用Matplotlib绘图：

>>> import matplotlib.pyplot as plt

>>> fig =plt.figure()

>>> ax = fig.add_subplot(111)

>>> ax.plot(xSort [:,1],yHat[srtInd])

[<matplotlib.lines.Line2D object at 0x03639550>]

>>> ax.scatter(xMat [:,1].flatten().A[0], mat (yArr).T.flatten().A[0] , s=2, C='red')

<matplotlib.collections.PathCollection object at 0x03859110>

>>> plt.show()

可以观察到如图2所示的效果。图2 给出了k在三种不同取值下的结果图。当k=1.0时权重很大，如同将所有的数据视为等权重，得出的最佳拟合直线与标准的回归一致。使用k=0.01得到了非常好的效果，抓住了数据的潜在模式。下图使用k=0.003纳入了太多的噪声点，拟合的直线与数据点过于贴近。所以，图2 中的最下图是过拟合的一个例子，而最上图则是欠拟合的一个例子。

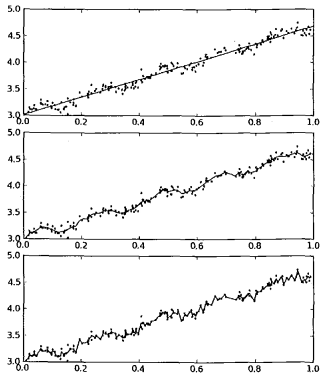
图2 使用3种不同平滑值绘出的局部加权线性回归结果。上图中的平滑参数k=1.0，中图k=0.01，下图k=0.003。可以看到，k=1.0时的模型效果与最小二乘法差不多，k=0.01时该模型可以挖出数据的潜在规律，而k=0.003时则考虑了太多的噪声，进而导致了过拟合现象

局部加权线性回归也存在一个问题，即增加了计算量，因为它对每个点做预测时都必须使用整个数据集。从图2 可以看出，k=0.01时可以得到很好的估计，但是同时看一下图1 中k=0.01的情况，就会发现大多数据点的权重都接近零。如果避免这些计算将可以减少程序运行时间，从而缓解

因计算量增加带来的问题。

责任编辑：admin